The production of magnetic flux is instantaneously proportional to the coil current i. Strictly speaking, this is only true for magnetic circuits which do not contain any electrically conductive magnetic flux paths. When the level of magnetic flux changes (i.e. is raised or lowered) in a path/medium which can also conduct electric current, such as iron, there will arise, by Faraday’s Law, circulating eddy currents.
(Faraday’s Law states that the voltage induced in any closed path in space is proportional to the time rate of change of the net magnetic flux which flows through the closed path cross-sectional area. If the closed path is in an electrically conducting medium, there will then be a circulating current around that closed path proportional to the generated voltage and the electrical conductivity of the medium).
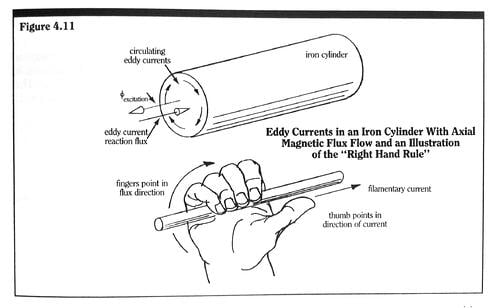
These eddy currents will, in turn, produce reaction magnetic flux which will tend to cancel out a portion of, or all of, the original excitation flux. The direction of eddy current flow can be deduced by the “ right hand rule” and by the requirement that the reaction magnetic flux produced by the eddy currents must flow in the opposite direction to the flow of excitation flux. Eddy current production in a simple cylindrical path in iron is illustrated in Figure 4.11.
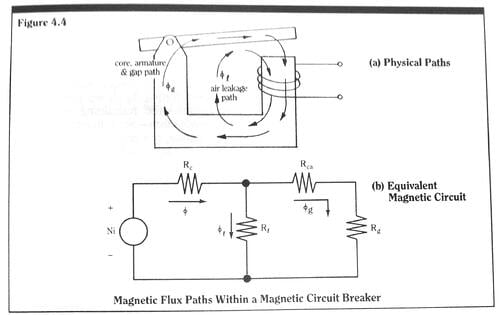
As a result of eddy currents, flux cannot be instantaneously produced in conducting mediums. There will always be a time “lag” between the flux flow and the exciting mmf. A simple magnetic equivalent circuit representation of this time-delay effect can be made by including “inductive” elements in series with reluctance elements which represent electrically conductive paths. For example, the structure shown in Figure 4.4 has two magnetic paths which are made up of ferromagnetic material: the core path and the armature path.
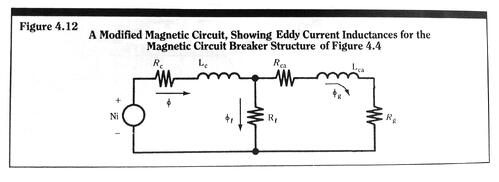
We include eddy current effects in these two paths by placing inductive elements in series with the reluctive elements which represent these paths. This modified circuit is shown in Figure 4.12.
The value of the inductive element for each magnetic path in a conducting medium is a function of the cross-sectional geometry of the path, the electrical conductivity of the material, and the effective length of the path. In the simple cylindrical structure of Figure 4.11, it can be easily shown that the equivalent eddy current inductance Le is given by
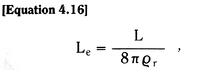
where L is the axial length of the conductor and ϱr is the electrical resistivity of the material. The magnetic reluctance of this path is
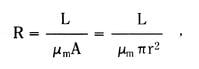
where µm is the magnetic permeability of the material , A is the cross-sectional area = πr2, and r is the cylinder radius. The magnetic time constant τe of this cylindrical path is then
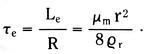
As typical values, let the material be a 1.5mm radius rod of magnetic iron with µm=˜ 2000µo and ϱr = 10-5Ω-cm. Thus,
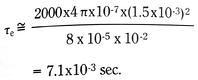
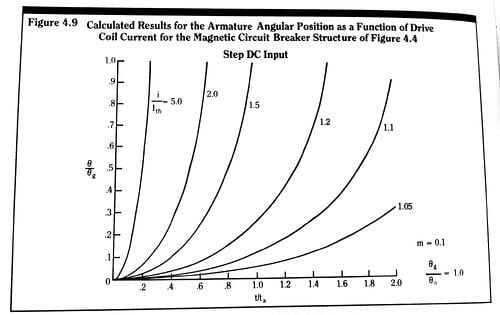
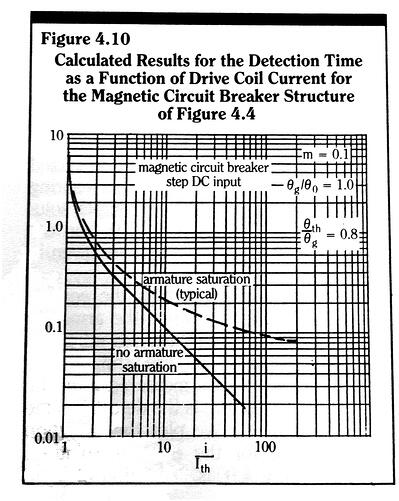
If such a rod is used as a magnetic core in a magnetic circuit breaker, and if we wish to accurately predict the breaker time response over time intervals of this magnitude, we must then necessarily include eddy current effects in our calculations. We can no longer use the simple results for the gap flux calculated from the static circuit of Figure 4.4. Rather, we must use the dynamic circuit of Figure 4.12. Results such as those given in Figures 4.9 and 4.10, calculated using static equivalent magnetic circuits, are optimistic at predicted operating time intervals equal to or less than the eddy current time constants of the structure elements.
For a rectangular cross-section magnetic path with side length ratio k, the equivalent eddy current inductance can be shown to be equal to
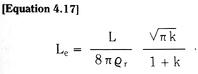
The path lengths of eddy currents in a rectangular cross-section magnetic conductor are longer than those in circular cross-section magnetic conductor. Thus, for equal electrical conductivities, the effective eddy current inductance in a rectangular conductor is lower.
To mitigate eddy current effects in magnetic materials, we see from Equations 4.16 and 4.17, that we should construct magnetic cores with
1) Magnetic irons (steels) with high resistivity values, (i.e. silicon steels). And
2) Very thin sheets (i.e. laminations) of magnetic steels stacked in the thin direction, and oriented such that the thin direction is perpendicular to the flow of magnetic flux.
The cost of such construction is only justified for devices which must operate at very high speeds (i.e. operating periods of the order of milliseconds).